9. Python: De basics#
Welkom bij de Python cursus. Vandaag gaan we aan de slag met programmeren in de browser. Als het goed is weet je hoe dat moet… (bekijk anders even de introductie)
9.1. Leerdoelen#
Werken met variabelen en types
Wiskundige bewerkingen
Libraries inladen en gebruiken
Numpy functies
Plotten
Exercise 9.1
Run de cell hieronder.
print('Hello, World!')
9.2. Variabelen, types en wiskundige bewerkingen#
Als je een beetje bekend bent met programmeren weet je al dat er verschillende variabele types zijn. Zo is er int voor de gehele getallen en float voor komma getallen. In sommige programma’s moet je precies vertellen wat voor een variabele je wilt hebben, maar Python kan dat zelf goed bepalen. Met het commando type kun je precies zien wat voor een typesoort je variabele is.
Exercise 9.2
Run de cell hieronder en bekijk eens wat voor verschillende types de vijf aangemaakte variabelen zijn. Kende je al deze types?
a = 1
b = '2'
c = 1.3
d = True
e = 'Ik ben een string'
type(a)
Variabele \(b\) is misschien niet wat we verwacht hadden. Doordat de type een string is, kunnen we ook niet zo makkelijk wiskundige bewerkingen doen.
Exercise 9.3
Probeer maar eens (in de cell hierboven) a + b te printen. Leg uit waarom dat niet werkt.
Een van de mogelijkheden die we hebben is de types te converteren. str(a) verandert het type van int naar str.
Exercise 9.4
In de cell hierboven verander het type van variabele zodat print(a+b) de waarde 3 terug geeft.
In de bovenste code cell werd Hello world geprint. Met de print functie kunnen we nog meer:
print('Variabele a + b = ', a + int(b))
Exercise 9.5
Leg uit waarom de eerste \(a\) en \(b\) niet als getal geprint worden.
Exercise 9.6
Wat gebeurt er wanneer je variabele \(c\) converteert naar het type integer?
Wat wellicht opvalt is dat je op deze manier dus strings en wiskundige bewerkingen kunt samenvoegen. Wat niet direct opvalt, is dat er kennelijk sprake is van een geheugen. In de hele code cell hebben we niet gespecificeerd wat \(a\) en \(b\) zijn. Die zijn in het geheugen opgeslagen. Wil je in een keer weten welke variabelen er zijn opgeslagen in het geheugen, en van welk type deze variabelen zijn, kun je het commando %whos gebruiken:
%whos
Nu we iets weten van de verschillende types kunnen we een voorspelling doen wat de uitkomst is van verschillende wiskundige bewerkingen.
Exercise 9.7
Voorspel wat de uitkomst is van onderstaande wiskundige bewerkingen. Bespreek de wiskundige bewerkingen die je niet begrijpt.
a = 2.5
b = 1.5
c = 3
d = 2
e = 4j
print(a+b)
print(a*c)
print(c**d)
print(a+b/d)
print(c%d)
print(int(a)+int(b))
print(int(a+b))
print(d+e)
Een data-type die we nog niet hebben gezien maar veel gebruikt wordt is de lijst. In een lijst kunnen we meer informatie (variabelen) opslaan. Die variabelen kunnen dan ook weer van verschillende type zijn.
Exercise 9.8
Bekijk de onderste lijst. Welke typen herken je? Controleer door de cell te runnen.
Person_1 = ['Feek','Pols','Lorentzweg',1,'Delft']
print(Person_1)
print(type(Person_1), type(Person_1[0]), type(Person_1[3]))
# Jouw aanpassing
Exercise 9.9
Er is een typefout geslopen in de voornaam van Person_1. Schrijf op regel 6 de code die deze fout herstelt (de persoon heet Freek).
Exercise 9.10
Kijk naar onderstaande code, wat verwacht je dat er geprint wordt?
a = [0,2,3]
print(a*2)
print(a[1]*2)
9.3. Numpy basics#
Om alles zelf te programmeren, is een enorme klus. We kunnen gelukkig veelal gebruik maken van code van anderen, opgeslagen in zogenaamde libraries. Een veel gebruikte library is NumPy (Numerical Python). Deze library biedt ondersteuning voor m.n. arrays (serie van getallen) en biedt een verzameling wiskundige functies om efficient met verschillende datastructuren te werken.
In de vorige opdracht verwachte je misschien dat \(a \cdot 2\) een lijst met de waarden [0 4 6] zou opleveren. Echter, de inhoud van lijst werd 2x geprint. Om welk de gewenste berekening te maken, kunnen we werken met numpy arrays. Daartoe moeten we eerst de numpy library inladen.
import numpy as np
We definiëren nu een numpy array en doen de eerdere berekening:
a = np.array([0, 2, 3])
print(a*2)
Stel nu dat we een rij getallen willen maken van 0 tot 100 met stappen van 1, gaan we dan alle getallen opschrijven? Zeker niet, we kunnen ingebouwde numpy functies gebruiken:
array_1 = np.linspace(0,100,51)
print(array_1)
array_2 = np.arange(0,101,1)
print(array_2)
np.linspace(0,100,51) maakt een rij aan die start bij 0, eindigt bij 100 waarbij die ruimte verdeeld wordt over 51 stukjes.
np.arange(0,101,1) maakt een rij aan die start bij 0, eindigt bij 100 met stapjes met een stapgrootte van 1.
Omdat de computer begint te tellen met 0, is het verstandig om altijd even te kijken naar de rij die je gemaakt hebt om te controleren of de stapgrootte overeenkomt met wat je wilt.
Exercise 9.11
Maak een array van 0 t/m 100 met alleen de even getallen.
Maak een array van 100 t/m 1, dus [100, 99, .., 1]
# Jouw code
Op de website van Numpy vind je documentatie over alle mogelijke functies, dat zijn er nogal wat! Het is goed om bij vragen de documentatie te raadplegen. Hieronder een exercise om daar eens naar te kijken.
Exercise 9.12
Bereken van de onderstaande array de gemiddelde waarde en de standaard deviatie met behulp van de numpy functie.
exercise_array = np.random.uniform(-10,10,100)
# Jouw code
Exercise 9.13
Hieronder staan twee numpy arrays, de een met even getallen, de ander met oneven getallen. Voeg de twee arrays samen en sorteer ze zodat je een array krijgt met de getallen 0 t/m 100. Gebruik de numpy functie concatenate en sort.
even = np.arange(0,101,2)
oneven = np.arange(1,101,2)
Exercise 9.14
Nu willen we de functie \(f(x)=a \cdot x^2\) bekijken, met \(a =2.5\) en de waarden \(x = [0,3,6,9,12]\). Maak de bijbehorende code daarvoor.
# Jouw code
x =
a =
f =
9.3.1. Een array uitbreiden#
Het kunnen bewerken van arrays is een van de belangrijkste handelingen, daarvoor kennen we verschillende technieken:
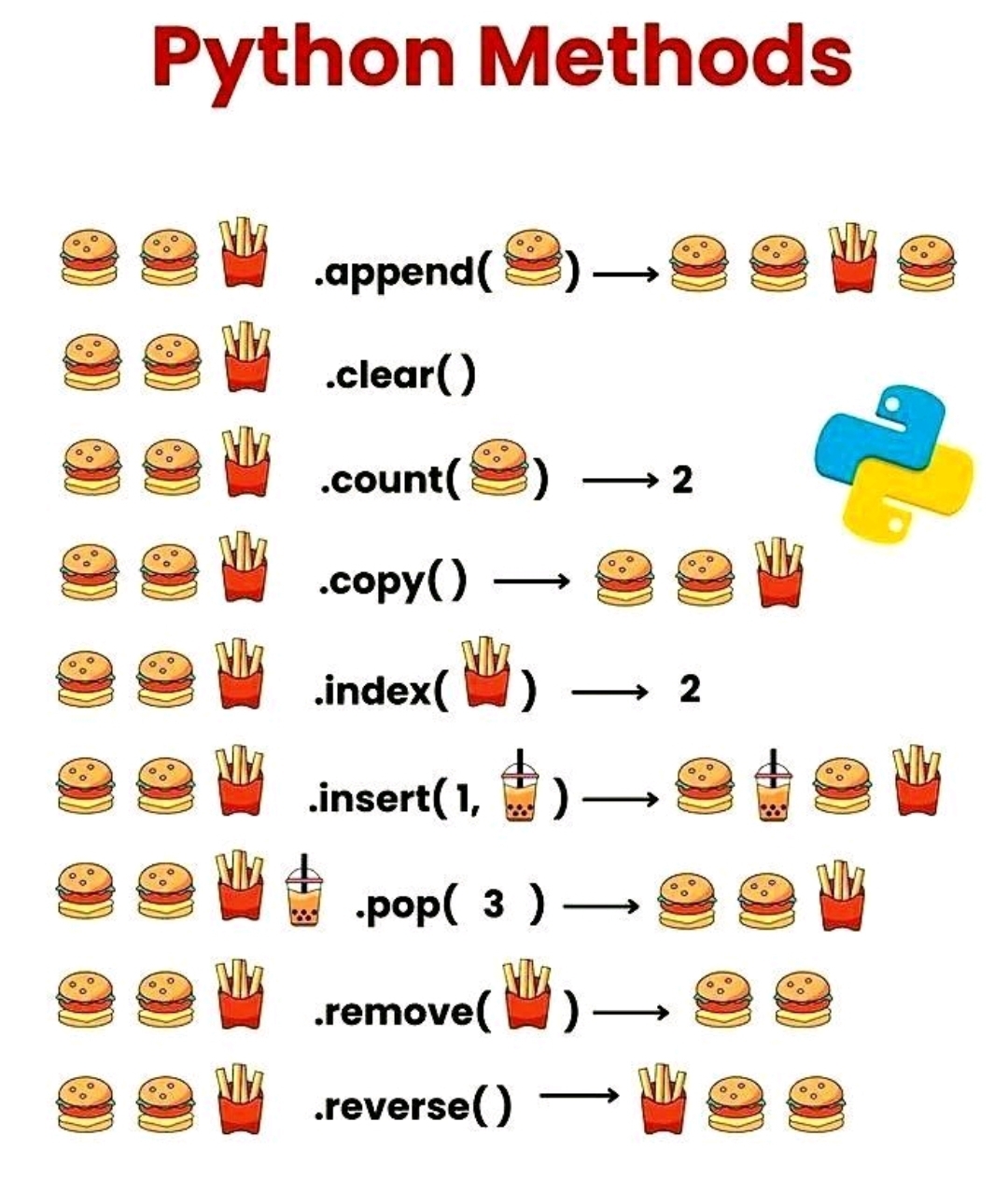
Fig. 9.1 Methoden om arrays te bewerken visueel uitgelegd#
slicen
Met slicen kun je een deel van een array selecteren op basis van indexen. Net als bij Python-lijsten kun je gebruik maken van de notatie [start:stop:step].
arr = np.array([0, 1, 2, 3, 4, 5])
print(arr[1:4]) # Output: [1 2 3]
print(arr[::2]) # Output: [0 2 4]
delete
Met np.delete() kun je specifieke elementen of rijen/kolommen uit een array verwijderen.
arr = np.array([1, 2, 3, 4, 5])
new_arr = np.delete(arr, 2) # Verwijder element op index 2
print(new_arr) # Output: [1 2 4 5]
append
Met np.append() kun je elementen aan een array toevoegen. Dit resulteert ook in een nieuwe array, omdat arrays een vaste grootte hebben.
arr = np.array([1, 2, 3])
new_arr = np.append(arr, [4, 5])
print(new_arr) # Output: [1 2 3 4 5]
concatenate
Met np.concatenate() kun je twee of meer arrays samenvoegen langs een bepaalde as.
arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])
result = np.concatenate((arr1, arr2))
print(result) # Output: [1 2 3 4 5 6]
Exercise 9.15
Je hebt de volgende array:
arr = np.array([10, 20, 30, 40, 50, 60, 70, 80])
Selecteer de elementen 30, 40, 50 uit de array en sla ze op in een nieuwe variabele genaamd subset1.
Selecteer alle oneven indexen uit de array en sla ze op in subset2.
Selecteer de array in omgekeerde volgorde (van 80 naar 10).
Controleer je antwoorden door de variabelen te printen.
# Jouw code
arr = np.array([10, 20, 30, 40, 50, 60, 70, 80])
Exercise 9.16
Gegeven de array:
arr1 = np.array([1, 2, 3, 4])
Voeg de elementen 5, 6, 7 toe aan arr1 en sla het resultaat op in een nieuwe array extended_arr.
Maak een nieuwe array arr2 = np.array([8, 9, 10]) en concateneer deze met arr1 tot een enkele array merged_arr.
Voeg het getal 0 aan het begin van de array arr1 toe.
Print alle resultaten en controleer je antwoorden.
# jouw code
arr1 = np.array([1, 2, 3, 4])
9.4. Plotten#
Nu we de basis van werken met Python en numpy arrays kennen, kunnen we kijken naar grafieken. Daarvoor maken we gebruik van de library matplotlib. Als je code hierboven goed is gegaan, staat hieronder de bijbehorende plot (na het runnen van de cel).
import matplotlib.pyplot as plt
plt.figure()
plt.xlabel('$x$')
plt.ylabel('$f(x)$')
plt.plot(x,f, 'k.',label=f'f(x)=%.1f*x^2' %a)
plt.grid()
plt.legend()
plt.xlim(0,15)
plt.ylim(0,max(f)+1)
plt.show()
Exercise 9.17
Bekijk de code hierboven en leg uit wat elke coderegel doet. Verbeter de grafiek (layout).
Exercise 9.18
Plot de functie \(f(x)=2 \cdot sin(4x)\) op het domein \([0,2\pi]\).
# Jouw code
9.5. Goede gewoonten#
Tot nu toe zijn we bezig geweest zonder ons druk te maken over de naamgeving van onze variabelen of onze code te voorzien van uitleg, zogenaamde meta-data. Het is een goede gewoonte om daar wel zorg aan te besteden, het de lezer - maar ook jezelf - makkelijk te maken door functies en variabelen zo te noemen dat ze makkelijk leesbaar zijn. Stukke code die lastiger te begrijpen zijn kun je voorzien van commentaar. Een # kun je gebruiken om commentaar toe te voegen.
Exercise 9.19
Lees de code in beide cellen. Welke code is makkelijker te volgen?
a = 5
b = 3
def s(a,b):
s = a+b
return print(s)
s(a,b)
8
# code om de som van twee getallen te berekenen
getal_1 = 5
getal_2 = 3
# functie om de som van twee getallen te berekenen
def som(getal1,getal2):
return getal1 + getal2
print(som(getal_1,getal_2))
8
